“Greg, Marcia, Peter, Jan, Bobby and Cindy go to a movie and sit next to each other in six adjacent seats. If Marcia and Jan will not sit next to each other, in how many different arrangements can the six people sit?” – GMAT Sample Question

Thankfully my standardized test-taking days are far behind me, but this kind of problem is typical of what one might find on an advanced level standardized test math section. It also so happens to be representative of what mathematicians refer to as a constraint problem.

Constraint problems (also commonly known as constraint satisfaction problems or CSPs) refer to a family of mathematical optimization problems. Wikipedia defines constraint satisfaction as follows: “…the process of finding a solution to a set of constraints that impose conditions that the variables must satisfy. A solution is therefore a set of values for the variables that satisfies all constraints.”

With that aside, I’d like to continue with a simple illustration that might help put some understanding behind these abstract definitions. For a moment, just imagine that you are the owner of a chocolate factory…

As a chocolate factory, your company is the sole supplier of three types of chocolate to a retailer whom we shall call “Bradburys.”  The three types of candy are Darkness™, Heaven™, and Therapy™ (these don’t actually exist as far as I know but can help with your imagination, YMMV). Now as CEO of your chocolate factory, your task is to maximize profit by keeping production costs low and output high. Seems straightforward, right? However with chocolate production, as in life, things are a little bit more complex.

Your factory has three machines – each producing only one type of candy. This limits the overall production for each type of candy to the capacity of the machine that can produce it. You also have a limited budget, and since chocolate doesn’t grow on trees (OK, technically cocoa does, but you know what I mean), you have to make financial decisions about what quantity of the different chocolates you are willing to produce. And just to make it even more complicated, some chocolate candies can be sold more profitably to Bradbury’s than others. Hmm, some tough decisions to make…

Turns out, not coincidentally, that this example qualifies as a perfect candidate for a constraint satisfaction problem. The problem is how much of the different quantities of chocolate to produce to maximize profit. The constraints are (1) having only three machines, (2) the budget, and (3) the profitability functions for each of the chocolates. Don’t worry, my hungry audience, we’ll come back to this example later, but for now we need to talk a little bit about programming…

The Microsoft Solver Foundation (MSF)

To help solve CSPs and other mathematical problems, Microsoft had kindly developed something called the Microsoft Solver Foundation^[1] (MSF). From their website, MSF “…is a set of development tools for mathematical simulation, optimization, and modeling that relies on a managed execution environment and the common language runtime (CLR).”

Seems like a great fit for helping us with our problem! So from here on out we are going to look at using MSF and later see how we can programatically apply it to the chocolate factory problem.

Getting Started With Microsoft Solver Foundation

For our intent and purposes, the Solver Foundation is really a single class library called Microsoft.Solver.Foundation.dll. To access the functionality of MSF, we simply need to include a reference to this file. However, there is no NuGet package for this library, it has to be downloaded from here and installed:

C:\Program Files (x86)\Reference Assemblies\Microsoft\Framework\.NETFramework\v4.0\Microsoft.Solver.Foundation.dll

While you’re trying to locate the MSF .DLL library you may also notice there is a “Samples” folder: (%USERPROFILE%\Documents\Microsoft Solver Foundation\Samples). This folder contains numerous code examples that use MSF to solve many different types of problems. If you find this topic interesting, I highly recommend spending some time playing around with the examples. Personally I’ve found them to be the best way to learn MSF.

Back to Our Chocolate Factory Example

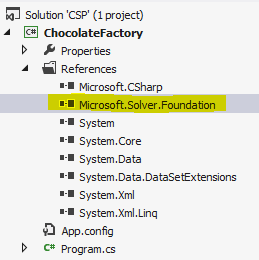Now, the next step is to set up our solution, so we create a blank solution and create a new C# Console project. (It doesn’t strictly have to be a Console project, but for ease of demonstration we’ll use one). Once we’ve created the project we add a reference to Microsoft.Solver.Foundation via the “Add Reference” context dialog:

Now this is where things get interesting. We will work in the Program.cs file and the first thing we need to do is initialize our Solver library and define our model and outputs. The way we do that in code is this:

So, two things to quickly note. The first is that we are defining a “solver.” MSF uses many different types of solvers for solving different types of problems. Once you have set up your problem, MSF by default will pick a solver for the type of problem it thinks you are trying to solve (in our case it would be the “Simplex” algorithm). You can think of a solver as the mechanism that actually abstracts the difficult math that goes on behind the scenes. From the perspective of design patterns, you can think of MSF as applying the “Strategy” pattern by delegating an algorithm at run-time to solve our particular problem. The second thing to understand is that we are defining our “outputs” or the format of what our answers should look like. To help the solver, we must define the type of output we are looking for. In this case it is a non-negative integer that will represent the quantity to produce of a given type of chocolate.

The second stage is where we can define all our constraints and our goal:

The tricky thing here is getting used to the way constraints are defined as algebraic statements of equalities/inequalities. But beyond that, the code is fairly self-explanatory.

Finally we tell the solver to “solve” our constraint problem:

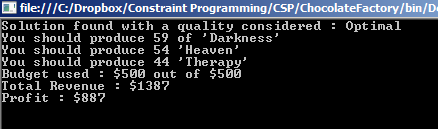
And we run our program display some output:

So from here we can see the respective quantities of what our little chocolate factory should produce. By tweaking the selling prices, machine output capacities, etc. you can get different “optimal” results. Fun stuff!

Hope you enjoyed this introduction to constraint satisfaction problems. My next blog post will be a continuation in this series where we look at solving the famous “map coloring” problem using constraint satisfaction techniques and MSF.